Overview
“I made the first one, I said, 'Let me see if I can make two.'
I made the second one, I said, 'Let me see if I can make three.'
I MADE THE THIRD ONE, I SAID, 'I’VE GOT A RHYTHM GOING.'”
-Kobe Bryant, on setting NBA single-game 3-point record
Across the game of basketball, players, coaches, and fans almost unanimously believe in the “hot-hand” phenomena: sometimes a player simply can’t miss. This phenomena is easily understood in the game of basketball, but describes in general a pattern in the human decision making process. We often attribute recent and consistent success at work, school, or some other activity to something beyond chance by saying “That person is on fire.”
I made the second one, I said, 'Let me see if I can make three.'
I MADE THE THIRD ONE, I SAID, 'I’VE GOT A RHYTHM GOING.'”
-Kobe Bryant, on setting NBA single-game 3-point record
Across the game of basketball, players, coaches, and fans almost unanimously believe in the “hot-hand” phenomena: sometimes a player simply can’t miss. This phenomena is easily understood in the game of basketball, but describes in general a pattern in the human decision making process. We often attribute recent and consistent success at work, school, or some other activity to something beyond chance by saying “That person is on fire.”
Until recently, the “Hot Hand Theory” was touted as the “Hot Hand Fallacy” by prominent cognitive psychologists and statisticians, chalked to an example of humans’ tendency to misunderstand randomness. Specifically, people tend to assume that the Law of Large Numbers applies to local trials, or a fallacious “Law of Small Numbers.”
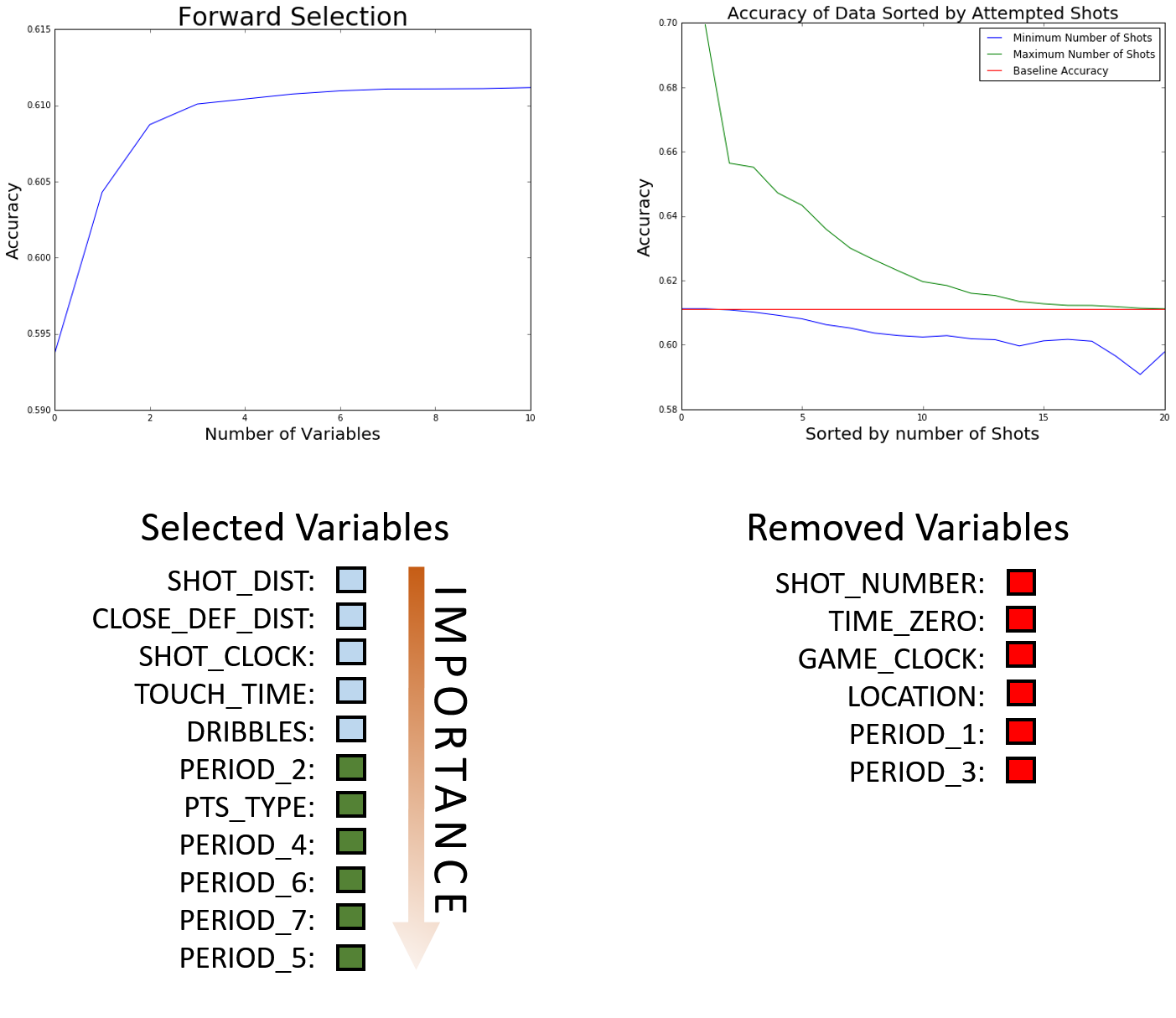
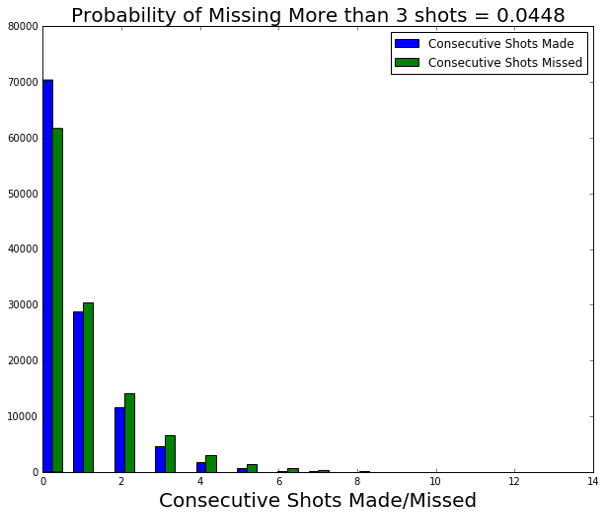
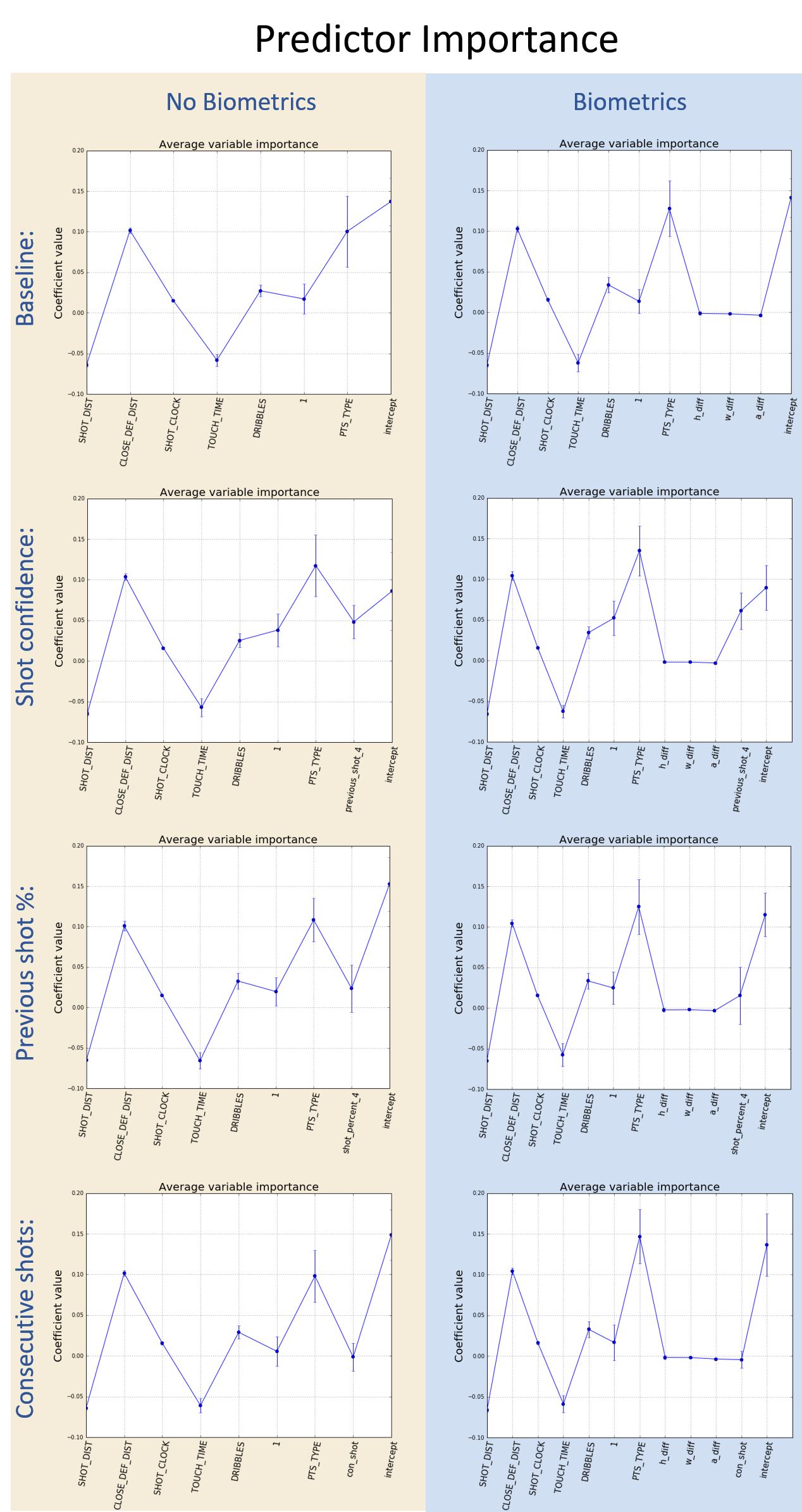
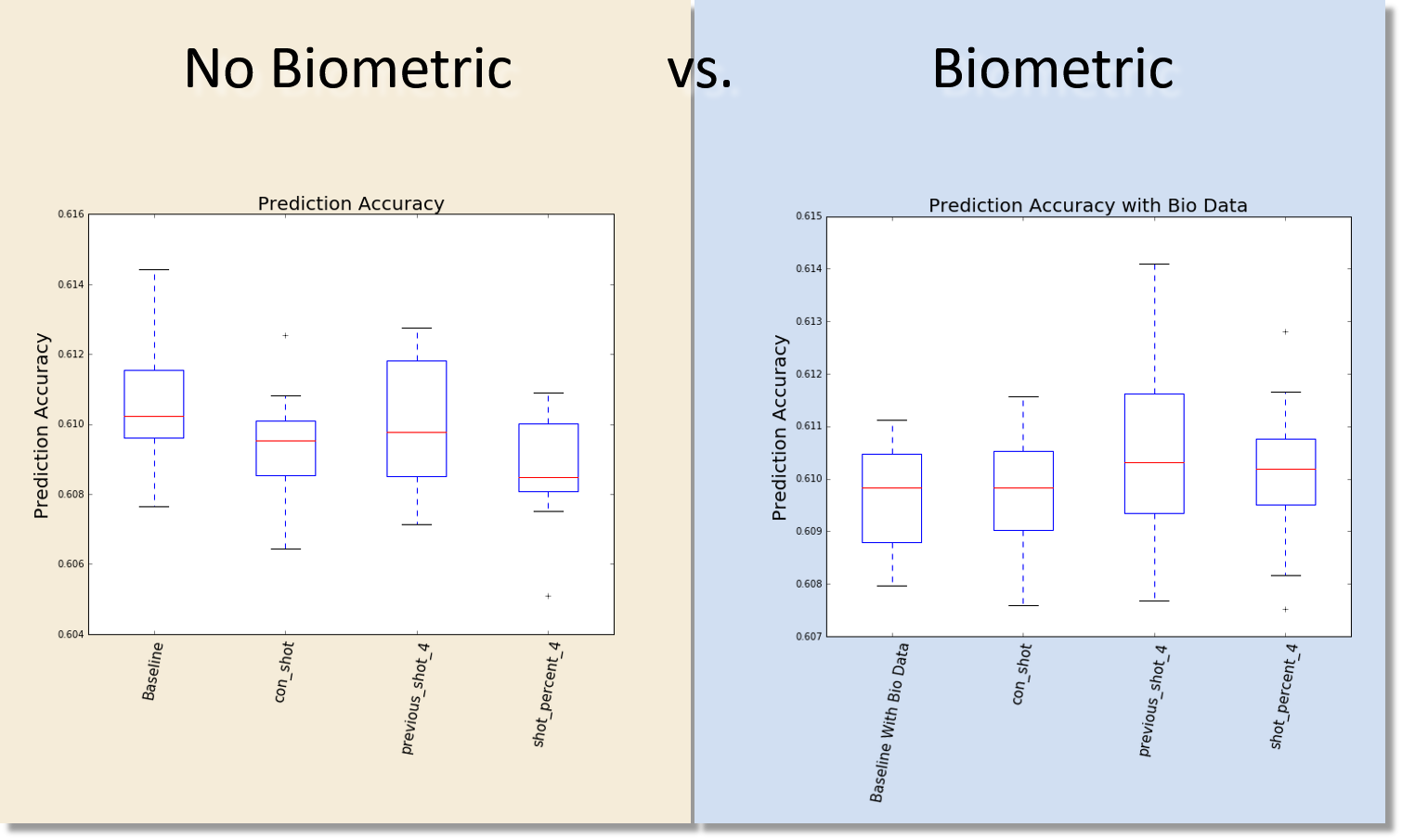
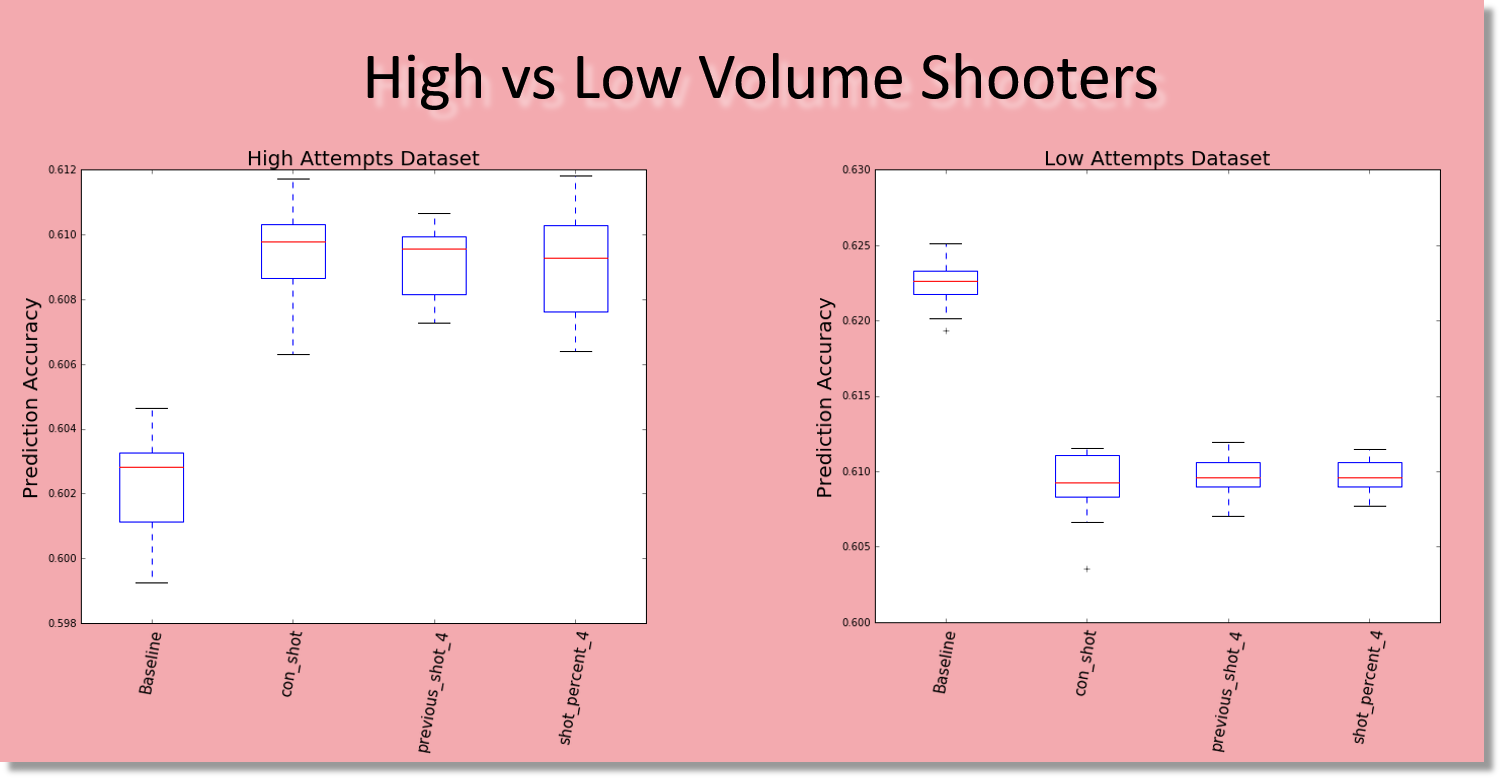
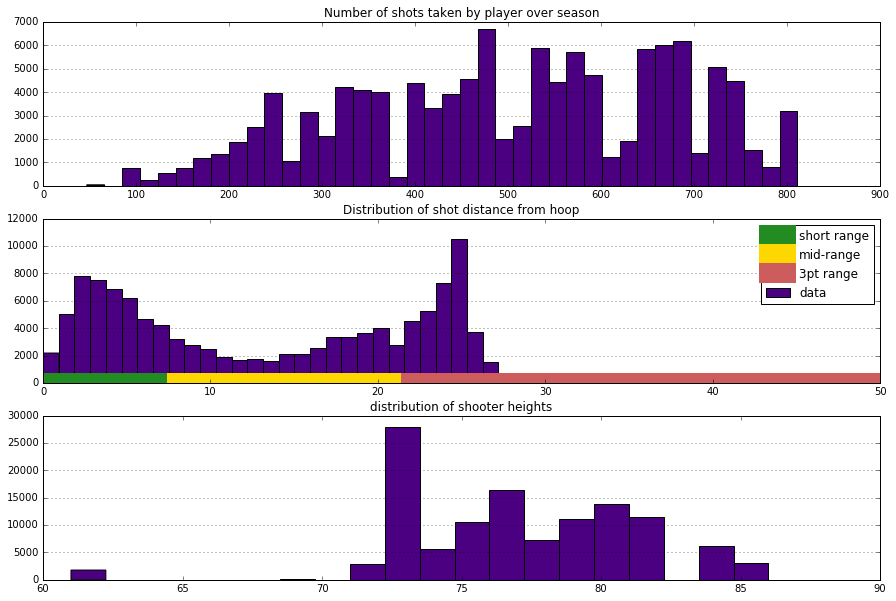
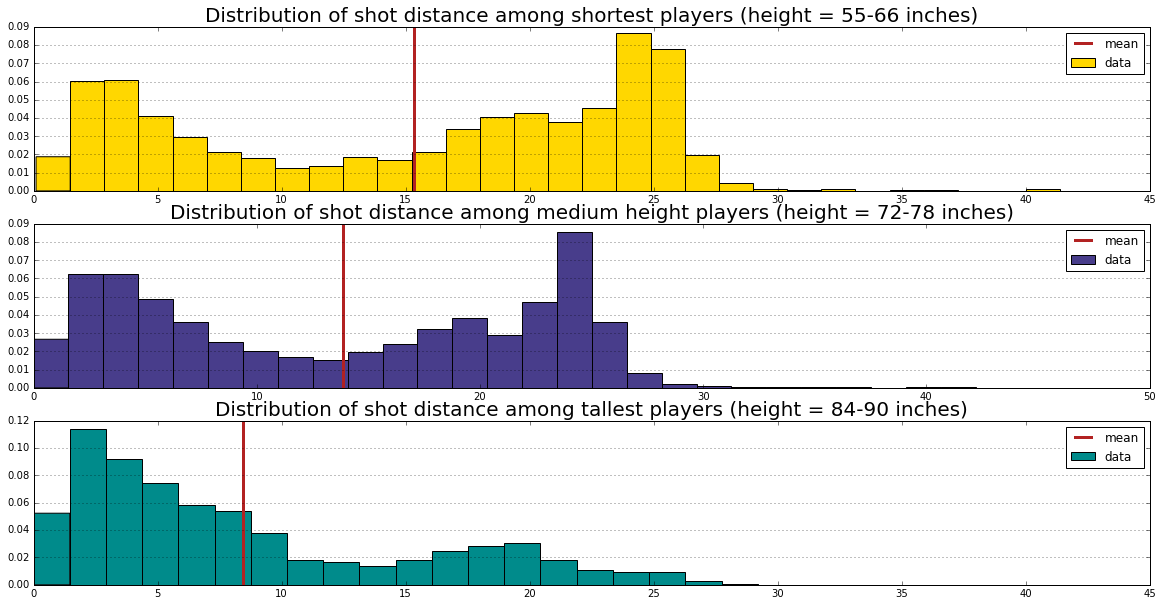
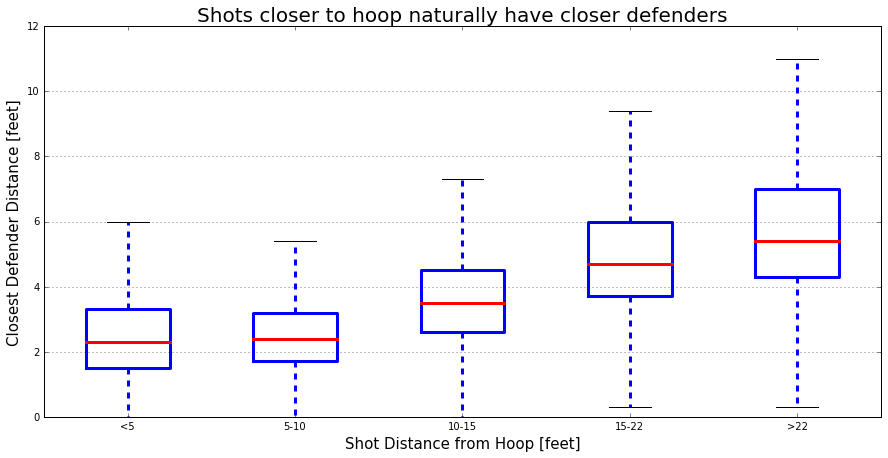
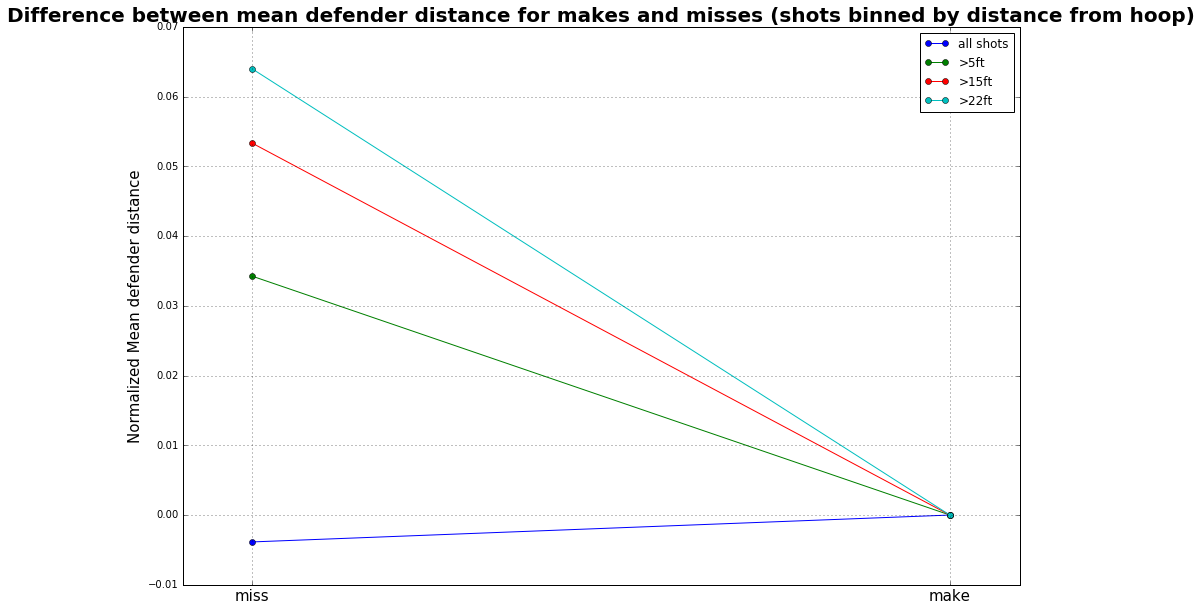
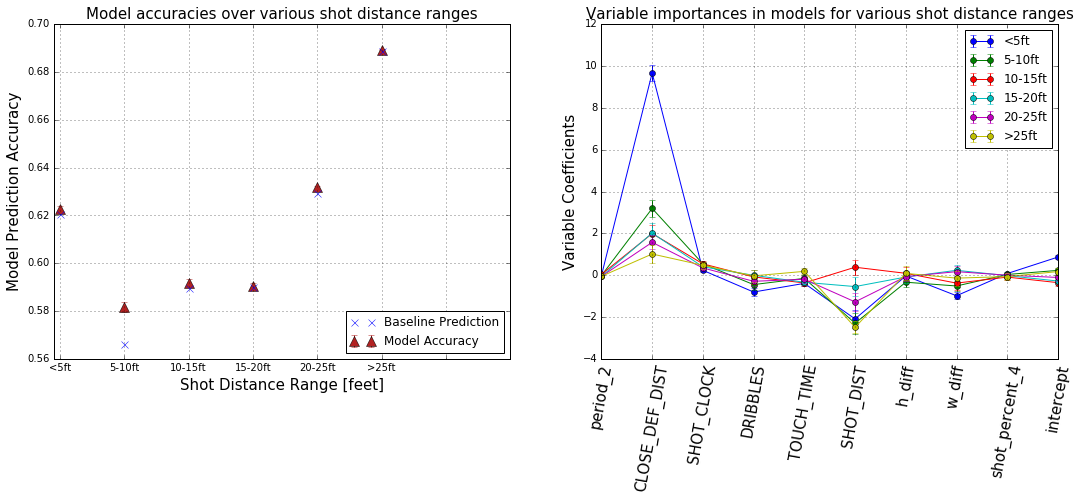
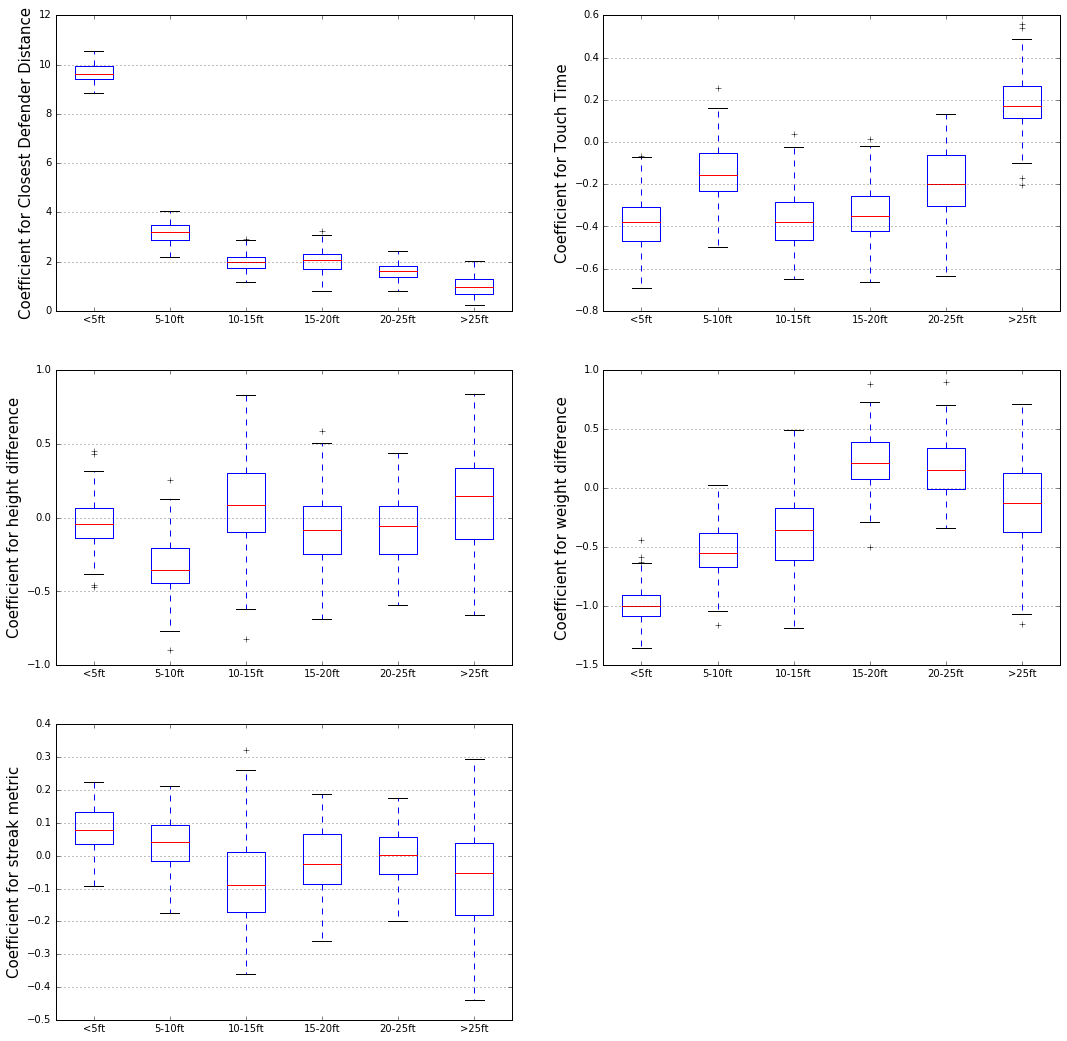
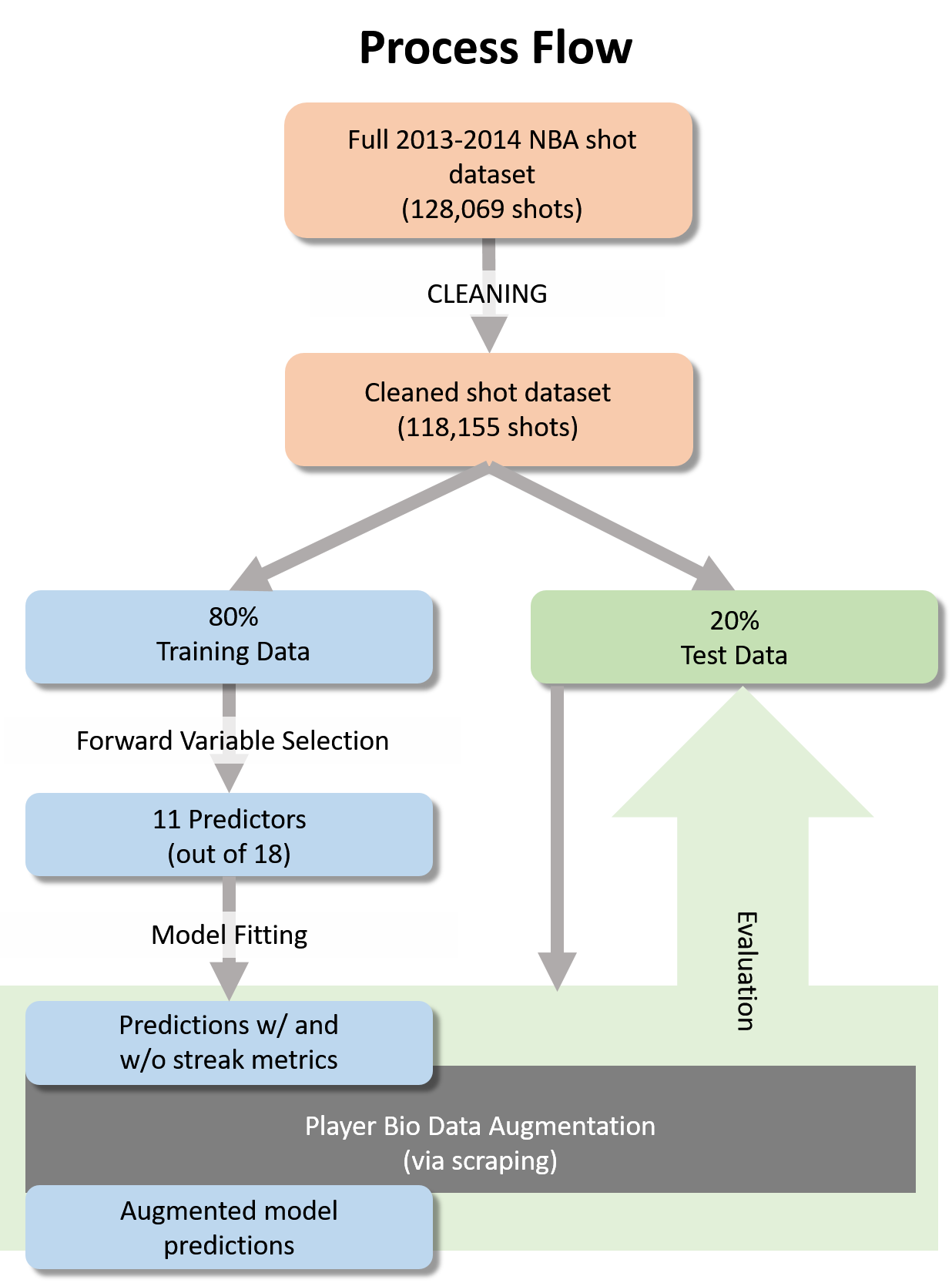
In our project, we are going to test if the hot hand theory is a true phenomena or just based on luck. Our work flow is showed bellow: